Possibilities and Probabilities
How “standard deviation” reveals the true odds of scoring a video poker jackpot
By Bill Burton
Last night I met my friend Rich at a casino. We hadn’t gotten together for a while, so we decided to play video poker so we could talk and catch up on recent events while we played. We’d been playing for about 20 minutes when Rich let out a yell. I looked over and saw that he had a royal flush on his screen.
“It’s a natural, it was dealt to me!” he exclaimed. “That’s the first time that I was ever dealt one. What are the odds?”
I told him the odds of being dealt a natural royal flush are one in 650,000 hands. But as I explained, this is only the mathematical probability of being dealt a natural. It does not mean that you will be dealt a natural every 650,000 hands. The mathematical probability of drawing to a royal flush is actually much better: one in every 40,000 hands. These figures are based on playing perfect optimal strategy, with each draw giving you the best mathematical return.
Standard Deviation
Of course nobody will get a royal flush in exactly 40,000 hands. It may happen in a fewer number of hands, or it may take longer. The easiest way to illustrate this is with the simple coin flip.
The odds of flipping a coin and having it land on heads is 50/50; however, if you flip a coin 100 times it would be rare to come up with exactly 50 heads and 50 tails. You could possibly end up with 75 heads and 25 tails. This is because a sampling of only 100 flips is very short, and anything can happen. If you flip a coin 1,000 times, it’s still unlikely that you’ll end up with an equal number of heads and tails.
The reason for this is a mathematical principle called “standard deviation.” Standard deviation is a statistical value used to determine how spread out the data in a sample is, and how close individual data points are to the mean, or average. Some of you may remember seeing a demonstration back in your high school days of ping pong balls being dropped down a board, similar to the Plinko game on the “Price Is Right” television show. The majority of the balls group in the center, while others bounce to the left or right of the center, forming a bell curve.
One standard deviation will cover 34.1 % of the curve to the left and right of the center line. In other words, it shows what will happen about two-thirds of the time. Two standard deviations cover what will happen 95% of the time. Three standard deviations cover 99.7% of what can happen.
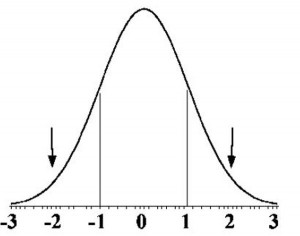
The formula for calculating standard deviation uses square roots and other algebra equations which can be looked up if you’re interested in doing the calculations. The main reason to have a general understanding of standard deviation is so that you’ll have a more realistic expectation of what you might encounter when playing a game like video poker.
When you flip a coin 1,000 times, the odds are 50/50—but to get a truer sense of the outcome, we look at the standard deviation. One standard deviation is about 68%, so we can expect that we’ll flip somewhere between 452–548 heads.
Now we can use standard deviation to calculate the range of drawing a royal flush based on the number of hands we play. If you were to play 200,000 hands of video poker and the probability of drawing a royal flush is one in 40,000, you would expect to get five royal flushes—but due to standard deviation, the true probabilities will be different.
We can illustrate this by sampling 100 players who will each play 200,000 hands of video poker. At the end of that time, 68 of the players will have drawn between two to six royal flushes, which is one standard deviation. 26 players will have drawn zero to eight royals, which represents two standard deviations; and the other six players would have drawn from zero to over eight royals. (Since we can’t have a “partial person,” I rounded off the number of players in this example)
Droughts Happen
I’ve gone more than a year between royal flushes. Although I don’t count the exact number of hands I play, I do keep a log of the amount of time that I play during each of my sessions. I know approximately how many hands I play per hour, so I can get an estimate of the total number of hands that I’ve played.
I estimated that I played about 285,000 hands without a royal flush. This placed me in the upper end of two standard deviations away from the norm, and since the majority of this play was at the same casino, had I not had an understanding that this was just a normal part of the distribution curve, I could have easily jumped to the conclusion that the machines were “rigged.”
I often hear this complaint from players, and they’re skeptical when I explain that droughts not as uncommon as they think.
Lightning Strikes Twice
After Rich and I had our conversation about the odds of him drawing a natural royal flush, I told him that the one thing I miss with the coinless machines is the hand paid jackpots. Although I don’t miss waiting for a hopper fill when cashing out, I do miss having the attendants come over and count out those hundred dollar bills. Maybe this is because the time spent waiting to get paid gave me more time to savor my win.
Nowadays, with the ticket-in, ticket-out machines, the winnings from your royal flush just get added to your credits, and you’re free to play your next hand. I no sooner said this when Rich yelled again. This time he had held two cards, and drew his second royal in the span of 20 hands!
He just looked at me and said, “If I had to wait for a hand paid jackpot, I never would have gotten my second royal.”
Point taken. I couldn’t argue with him there.
Until next time, remember: “Luck comes and goes…Knowledge Stays Forever!”
Bill Burton is a writer for the Casino Gambling Guide at About.com. (www.casinogambling.about.com). He is the author of 1,000 Best Casino Gambling Secrets and Get the Edge at Low Limit Texas Hold’em. He is also an instructor for Golden Touch Craps.(www.goldentouchcraps.com).


