Understanding Expected Value:
Learn to expect the expected
By Henry Tamburin
I often use the term expected value (or EV) when I’m writing about the best video poker playing strategies. Even though EV is foreign to most players, smart players know what that term means and how it is determined.
EV is a mathematically precise term that represents the average return that you can expect when holding a group of cards in a hand. You’ll always do better playing video poker (meaning win more or lose less money) if you choose the holding that has the highest EV.
The math used to calculate EV is not very complicated and I’ll show in the following example how it’s done.
Suppose you are playing 9/6 Jacks or Better and you are dealt the following hand. How would you play it?
 There are two possible holds:
There are two possible holds:
Hold #1: Hold the grouping 5-6-7-8 and draw one card, hoping for a straight or
Hold #2: Hold the grouping 2-5-7-8 and draw one card, hoping for a flush.
Assuming you bet five coins, here’s how to calculate the EVs for the two holds. (Note: Remember that the hand began with a virtual deck of 52 cards, five cards were randomly selected from this shuffled deck for your initial hand, leaving 47 unplayed cards for the subsequent draw.)
Hold #1
We hold the four-card straight 5-6-7-8 and draw one card. We are hoping to draw either a 4 or a 9 that would give us a straight. In the 47 unplayed cards, there are four 4s and four 9s. Therefore, the probability of drawing a 4 or 9 is the ratio 8 over 47 (8/47). The payoff for a straight is 20 coins. The EV is the product of the probability of getting the cards you need (8/47) times the payoff (20 coins). When you do the multiplication, you arrive at an EV of 3.40, which means, on average, you will get back 3.40 coins from the 5 coins you wagered. Therefore, eight times out of every 47 times on average that you draw to this hand, you stand to win 20 coins each time, whereas 39 times you will win nothing (meaning your draw card won’t be a 4 or 9). Therefore, think of the 3.40 EV for this hold as an average payback you can expect after an infinite number of trials.
Hold #2
This time we are going to hold the four-card flush (2-5-7-8) and draw one card from the 47 unplayed cards. We need any diamond-suited card to give us a flush, and there are nine left in the 47 cards. (There are 13 diamond-suited cards per deck minus the four diamond cards in our initial hand leaving nine diamond-suited cards). Therefore, the EV for this one card draw is the probability of drawing a diamond-suited card (9/47) times the payoff for the flush (30 coins), yielding an EV of 5.74, meaning, on average, you can expect to win 5.74 coins after many trials.
If you are a dollar player, the above EV’s mean you can expect a return of $5.74 on average for your $5 bet when you hold the four-card flush, and only $3.40 for holding the four-card straight. Clearly, holding the four-card flush is a more profitable play in the long run because it has a higher EV than holding the four-card straight.
Often times, we are faced with several options as to which cards to hold or to simply hold them all. Take this hand, for example.
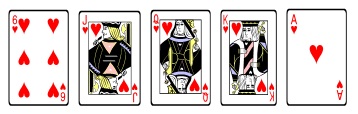 The majority of video poker players would hold the five-card flush for the guaranteed 30-coin payoff. The EV for this hold is simply 30. If instead you held hold the four-card royal flush, you, of course, would be hoping to get the ten of hearts for a royal flush. However, you could draw a different suited heart for a flush, or another picture card or ace to form a high pair, or a ten of a different suit for a straight. In fact, the table below lists the possible number of final hands that could occur with a one-card draw, the probability of getting each of these final hands, and the payoff for each final hand.
The majority of video poker players would hold the five-card flush for the guaranteed 30-coin payoff. The EV for this hold is simply 30. If instead you held hold the four-card royal flush, you, of course, would be hoping to get the ten of hearts for a royal flush. However, you could draw a different suited heart for a flush, or another picture card or ace to form a high pair, or a ten of a different suit for a straight. In fact, the table below lists the possible number of final hands that could occur with a one-card draw, the probability of getting each of these final hands, and the payoff for each final hand.
One Card Draw Hands
| FINAL HAND | PROBABILITY (1) | PAYOFF (2) | 1 x 2 |
| Royal Flush | 1/47 | 4000 coins | 85.11 |
| Flush | 7/47 | 30 coins | 4.46 |
| Straight | 3/47 | 20 coins | 1.28 |
| High Pair | 12/47 | 5 | 1.28 |
| EV | 92.13 |
To calculate the EV for holding the four-card royal flush and drawing a single card, you multiply the probability of getting the specific winning hand times its payoff. You do this for all the possible final hands and then add up the result, which computes to 92.13. This means you will win $92.13 for every five-dollar bet after many trials if you break up the paying flush, hold the four-card royal instead, and draw one card. Winning $92.13, on average, is much better than winning $30; therefore, the best strategy for this hand is to hold the four-card royal flush. (This is an example where in the long run, you’ll win more money by not holding a guaranteed paying hand.)
The calculation of EV for a two-card draw is more complicated because there are 1,081 combinations of winning hands (for a three-card draw, it is 16,215). However, high-speed computers can easily compute the EV for different holds in milliseconds. (In fact, the popular Video Poker For Winners software training program computes the EV for different holds in any selected hand by using the “Analyze This Hand” function.)
It’s not necessary to memorize the EVs for different holds. Strategy tables and strategy cards rank the card holdings from highest EV to lowest. All you have to do is to select the holding that is highest in the table for any hand and you’ll always be making the correct play. It’s that easy.
Tamburin Tip of the Month
How would play these hands if you were playing Jacks or Better?
 Both hands contain a four-card inside straight with three-high cards (i.e., the A-K-Q.) For the top hand, the card combination with the highest EV is to hold the 10-Q-K-A (EV 2.66). In the bottom hand, you have two choices. You can either hold the four-card inside straight (10-Q-K-A) or hold the two suited high cards (K-Q). The EV for these two holds is 2.66 and 2.89 respectively; meaning, holding the two-suited high cards is the better play because it has a slightly higher EV. The general rule when you are dealt the above hand is this: Hold the four-card inside straight with three high cards unless two high cards are suited. If the latter is the case, you should hold the two suited high cards.
Both hands contain a four-card inside straight with three-high cards (i.e., the A-K-Q.) For the top hand, the card combination with the highest EV is to hold the 10-Q-K-A (EV 2.66). In the bottom hand, you have two choices. You can either hold the four-card inside straight (10-Q-K-A) or hold the two suited high cards (K-Q). The EV for these two holds is 2.66 and 2.89 respectively; meaning, holding the two-suited high cards is the better play because it has a slightly higher EV. The general rule when you are dealt the above hand is this: Hold the four-card inside straight with three high cards unless two high cards are suited. If the latter is the case, you should hold the two suited high cards.
————————————————————————————————————-
Henry Tamburin is a blackjack and video poker expert. He is the host of the smartgaming.com website and the editor of the Blackjack Insider newsletter (for a free three-month subscription, visit www.bjinsider.com/freetrial). For a free copy of his Casino Gambling Catalog, which contains books, strategy cards, and software for video poker players, call toll free 1-888-353-3234, or visit the web store at smartgaming.com.


