UNDERSTANDING DEUCES
How jackpots work in the Deuces games
By John Grochowski
 When video poker rocketed to popularity in the 1980s after its invention by Si Redd in the 1970s, a couple of things became apparent that still influence games today:
When video poker rocketed to popularity in the 1980s after its invention by Si Redd in the 1970s, a couple of things became apparent that still influence games today:
Players will flock to video games that give them frequent paybacks and a good shot to win.
Players love the chance at a modest secondary jackpot that comes up fairly often, and will accept less in smaller pays to get it.
Deuces Wild came to the fore early as an enduring blend of those factors. In its original, full-pay, 100.8 percent- return version—a rare treat in the few casinos that still have it—Deuces Wild pays off on 45.3 percent of hands. Slot players of the time were used to three-reel stepper slots with paybacks on about 9 percent to 14 percent of spins, so that video poker hit frequency was an attraction in itself.
The primary jackpot remains 4,000 coins for a five-coin bet when you draw a royal flush with no wild cards. There’s an added attraction in a secondary jackpot of 1,000 coins for four deuces. On a quarter machine, that’s $250, enough to make a player on a modest budget feel as if they’ve had a nice day’s win. And it feels as if it’s attainable, coming up an average of about once per 4,909 hands.
Compare that to the first mega-popular video poker game, 9-6 Jacks or Better with its 99.5 percent return with expert play. The only jackpot that tops $100 for a quarter player is the royal flush, and that’s a 1 in 40,391 shot—it feels like miracle time when you draw one. The next biggest payoff, on straight flushes, is only 250 coins, or $62.50 for a quarter player, and even that comes up only once per 9,148 hands.
That reasonably large, attainable jackpot on four 2s proved incredibly popular. International Game Technology adapted it to non-wild card games with secondary jackpots on four aces, such as Bonus Poker, Double Bonus Poker, Double Double Bonus Poker, and many more.
Deuces Wild spawned its own family of games, with Double Pay Deuces, Triple Pay Deuces, Loose Deuces and others.
The derived Deuces games build on the original concept with even bigger secondary jackpots. Instead of 1,000 coins, four 2s are worth 2,000 on Double Pay Deuces, 2,500 on Loose Deuces and 3,000 on Triple Pay Deuces.
Naturally enough, that leads to questions from players who wonder just how the games can afford to pay these jackpots. Are different games dealing 2s with different frequencies?
One reader wrote earlier this year to ask, “I have long wondered how the deuces are controlled in video poker games where the payoffs are greater for four deuces. If deuce distribution wasn’t controlled, why then would there be different payoffs for the same hand?”
The games don’t deal cards differently. Every card has an equal chance of being dealt on every hand, and if players charted the appearance of deuces over a very long time—hundreds of thousands of plays—they would see that they come up with the same frequency on all games. Every card has an equal chance of being dealt on every hand.
Let’s look at the frequency of four-2 hands in four different Deuces games. We won’t use full-pay Deuces here because it’s so rare. Instead, let’s use a common Deuces version, the one sometimes called “Illinois” or “Airport” Deuces, which returns 98.9 percent with expert play. For comparison, we’ll use equivalent games— a 99.2 percent version of Double Deuces, a 99.2 percent version of Loose Deuces and a 98.9 percent version of Triple Deuces.
Table 1 lists payoff per coin but assuming a five-coin bet. That’s to get the full natural royal payoff, which is only 250-for-1 if you bet less than the max but jumps to 800-for-1, or 4,000 total, for a five- coin wager.
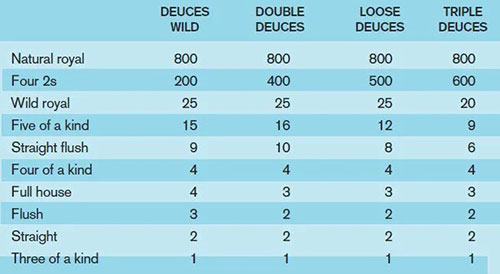
Depending on which version you play, four 2s could bring you 1,000, 2,000, 2,500 or 3,000 coins per five coins wagered. The reader who raised the question wondered if that meant you drew the 2s less often on the bigger-jackpot game.
It doesn’t work that way. Assuming expert strategy, on this version of Deuces Wild, you’ll draw the 2s an average of once per 5,348 hands, while on the other games listed the 2s come once per 4,764 hands on Double Deuces, 4,674 on Loose Deuces and 4,457 on Triple Deuces.
We draw four 2s MORE often, not less often, on the games with the bigger jackpots. That’s because expert strategy changes to chase the 2s more often when the jackpots are bigger.
That particularly applies to straight flush hands with one or two 2s. For an example, let’s say you’re dealt two 2s along with 8- 9 of diamonds and a King of clubs. In Triple Deuces, with the largest four- deuce jackpot and a reduced pay on straight flushes, your average return per five coins wagered will be 19.7 coins if you hold the 2s and discard everything else, and only 13.5 if you also hold the two diamonds. In Loose Deuces, it’s a little closer call, at 18.9 for 2-2 and 15.2 for 2-2-8-9, and closer still on Double Deuces at 17.9 vs. 16.9.

But on this Deuces Wild version, with the smallest 2s jackpot and the 3-for-1 flush pay that’s cut above the other games, the situation flips. Average returns are 16.5 on the four-card straight flush and only 15.2 on the 2s by themselves.
Such strategy flips, chasing 2s more often when they pay more, are why four-2 hands come more often on the bigger jackpot games.
That still leaves the reader’s underlying question: If the bigger-jackpot games don’t deal fewer deuces, how are they able to offer the bigger payoffs?
The key, of course, lies in the rest of the pay tables, just as it does in other video poker games.
It’s the same situation players are used to in other games, such as Double Bonus Poker vs. Bonus Poker. Four aces on Double Bonus pays 800 coins for a five-coin bet, but on Bonus Poker four aces pay only 400 coins.
The game doesn’t deal fewer aces on Double Bonus to make up the difference. The bigger payoff is offset by changes in the remainder of the pay table, mainly by two pairs paying 2-for-1 on Bonus, but only 1-for-1 on Double Bonus.
It’s the same deal on Deuces games. The jackpots are just offset by lower pays on hands that occur more often.
Note that in the pay tables above, the game with the lowest deuces jackpot also is the only game that pays 3-for-1 on flushes. That has a huge impact. In that Deuces version, flushes come up an average of once per 48.9 hands. Flushes come up more than 100 times as often as four 2s.
Similarly, the lowest deuces jackpot game also is the only one with a 4-for-1 payoff on full houses. Those come up once per 38.2 hands, and you’ll get about 140 full houses for each time you draw four deuces.
Flushes and full houses come up less often on the other games as expert strategy changes to account for the pay table changes, but even so on Double Deuces, you’ll see about 72 flushes and 101 full houses for every four deuces, while it’s 76 flushes and 99 full houses on Loose Deuces and 68 flushes and 95 full houses on Triple Deuces.
Reducing payoffs on those hands goes a long way toward funding bigger deuce jackpots on the other games. You also see reduced five of a kind and straight flush pays on Loose Deuces and Triple Deuces, and lower-paying wild royals on Triple Deuces.
The pay table shifts are plenty. There doesn’t have to be any reduction in the frequency of deuces. The random number generator just keeps generating random results, and lets the pay table take care of the rest.


